Question

Please help me i need this before Wednesday , will mark brainiliest and I don’t know how to solve it

Answer 1

The price of one adult ticket is $11 and the price of one student ticket is $6.

Explanation:

We can write a system of equations to represent the situation. Let a represent the price of adult tickets sold and s represent the price of student tickets.

On the first day, nine adult tickets and 12 student tickets were sold for a total of $171. Hence:

`\displaystyle 9a + 12s = 171`

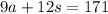
And on the second day, 13 adult tickets and 14 student tickets were sold for a total of $227. Hence:

`\displaystyle 13a + 14s = 227`

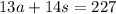
This yields a system of equations:

`\displaystyle \left\{ \begin{array}{l} 9a + 12s = 171 \\ 13a + 14s = 227\end{array}`

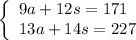
We can solve using elimination. Note that the LCM of 12 and 14 is 84. Hence, we can multiply the first equation by -7 and the second by 6:

`\displaystyle \left\{ \begin{array}{l} -63a + 84s = -1197 \\ 78a + 84s = 1362\end{array}`

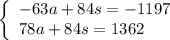
Adding the two equations together now produces:

`\displaystyle \begin{aligned} (-63a + 84s) + (78a + 84s) &= (-1197) + (1362) \\ 15a &= 165 \\ a&=11\end{aligned}`

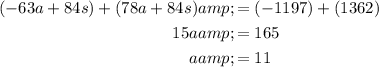
Therefore, the price of one adult ticket is $11.

To find the price of one student ticket, use either one of the original equations:

`\displaystyle \begin{aligned} 9a + 12s &= 171 \\ 9(11) + 12s &= 171 \\ 99 + 12s &= 171 \\ 12s &= 72 \\ s &= 6 \end{aligned}`

In conclusion, the price of one adult ticket is $11 and the price of one student ticket is $6.