Question

The College Board estimated the mean SAT score in 2016 was 1083 points with a standard deviation of 193 points. Assume

the distribution of SAT scores is unknown and a sample classroom, with size n = 30, was randomly drawn from
the population of SAT takers. Using the Central Limit Theorem for Means, what is the standard deviation for the sample
mean distribution?

Answer 1

Approximately
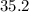`35.2` points.

Explanation:

Let random variables
`X_(1),\, \dots,\, X_(30)` denote the score of those
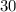`30` test-takers. These random variables are independently and identically distributed. In other words, the scores follow the same distribution and are independent from one other.

While the exact distribution of each score is unknown, the mean and variance of this distribution are given:
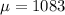`\mu = 1083` and
`\sigma = 193`.

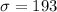By the Central Limit Theorem, the mean (average)
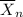`\overline{X}_(n)` of a sufficiently large number of such observations would follow a normal distribution. The mean of that distribution would be
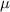`\mu` (same as the mean of the observations) while the variance
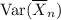`{\rm Var}(\overline{X}_(n))` would be
`(\sigma^(2) / n)`.

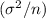Take the square root of variance to find the value of the corresponding standard deviation:

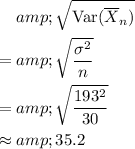`\begin{aligned}& \sqrt{{\rm Var}(\overline{X}_(n))} \\ =\; & \sqrt{(\sigma^(2))/(n)} \\ =\; & \sqrt{(193^(2))/(30)}\\ \approx\; & 35.2\end{aligned}`.