1 Answer

Tomglynch · Answer 1 · 2023-07-16T11:01:05+0000

We are given with the function
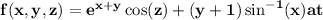${\bf{f(x,y,z)=e^(x+y)\cos (z)+(y+1)\sin^(-1)(x)at}}$ and we need to find
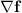${\bf \\abla f}$ , that's nothing but just the gradient of f(x,y,z) . But before starting let's recall ;

For a function F(x, y, z, ....) , the gradient is given by ;

${\boxed{\bf{\\abla F=(\partial F)/(\partial x)\hat{i}+(\partial F)/(\partial y)\hat{j}+(\partial F)/(\partial z)\hat{k}+\cdots}}}$

So , now let's calculate the partial derivatives of f(x, y, z) first with respect to x , y and z one after other .So consider ;

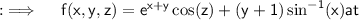
${:\implies \quad \sf f(x,y,z)=e^(x+y)\cos (z)+(y+1)\sin^(-1)(x)at}$

Partial differentiating both sides w.r.t.x will yield ;

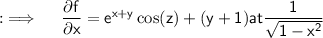
${:\implies \quad \sf (\partial f)/(\partial x)=e^(x+y)\cos (z)+(y+1)at\frac{1}{\sqrt{1-x^(2)}}}$

Simplifying will yield ;

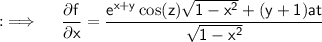
${:\implies \quad \sf (\partial f)/(\partial x)=\frac{e^(x+y)\cos (z)\sqrt{1-x^(2)}+(y+1)at}{\sqrt{1-x^(2)}}}$

Now again consider ;

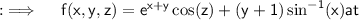
${:\implies \quad \sf f(x,y,z)=e^(x+y)\cos (z)+(y+1)\sin^(-1)(x)at}$

Partial differentiating both sides w.r.t.y will yield ;

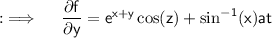
${:\implies \quad \sf (\partial f)/(\partial y)=e^(x+y)\cos (z)+\sin^(-1)(x)at}$

Now , again consider ;

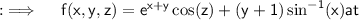
${:\implies \quad \sf f(x,y,z)=e^(x+y)\cos (z)+(y+1)\sin^(-1)(x)at}$

Partial differentiating both sides w.r.t.z will yield ;

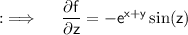
${:\implies \quad \sf (\partial f)/(\partial z)=-e^(x+y)\sin (z)}$

${:\implies \quad \bf \therefore \quad \underline{\underline{\\abla f=\bigg\{\frac{e^(x+y)\cos (z)\sqrt{1-x^(2)}+(y+1)at}{\sqrt{1-x^(2)}}\bigg\}\hat{i}+\bigg\{e^(x+y)\cos (z)+\sin^(-1)(x)at\bigg\}\hat{j}-\bigg\{e^(x+y)\sin (z)\bigg\}\hat{k}}}}$

This is the required answer