Question

Find the volume obtained when the shaded region is rotated
through 360' about the y-axis.​

Answer 1

Using the shell method, the volume is given by

`\displaystyle 2\pi \int_0^1 x(2-(x^2+1))\,\mathrm dx = 2\pi \int_0^1 (x-x^3)\,\mathrm dx`

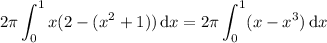
That is, each cylindrical shell with radius x from the axis of revolution has height equal to the vertical distance between the upper curve (y = 2) and the lower curve (y = x ² + 1). Then the area of this shell is 2πrh = 2π x (2 - (x ² + 1)).

Computing the integral gives the volume,

`\displaystyle 2\pi \int_0^1 (x - x^3)\,\mathrm dx = 2\pi\left(\frac{x^2}2-\frac{x^4}4\right)\bigg|_0^1 \\\\ = 2\pi \left(\frac12 - \frac14\right) \\\\ = \boxed{\frac\pi2}`