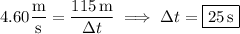By definition of average velocity,

If this object is under constant acceleration, then average velocity is also equal to the average of the initial and final velocities:
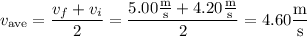
Then the time it takes for the object to travel 115 m with this average velocity is