Question

A reconnaissance plane flies 560 km away from its base at 602 m/s, then flies back to its base at 903 m/s.

What is its average speed?
Answer in units of m/s.

Answer 1

Approximately
`722\; \rm m\cdot s^(-1)`.

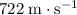Step-by-step explanation:

The average speed of a vehicle is calculated as:

`\displaystyle \text{average speed} = \frac{\text{total distance}}{\text{total time}}`.

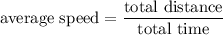In this question, the total distance is
`2 * 560\; \rm km = 1120\; \rm km`.

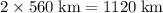The unit of the speeds in this question is meters per second, while the unit of distance is kilometers. Convert the unit of distance to meters:

`560 \; \rm km = 560 * 10^(3) \; \rm m = 5.6 * 10^(5)\; \rm m`.

`1120 \; \rm km = 1120 * 10^(3) \; \rm m = 1.12 * 10^(6)\; \rm m`.

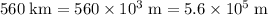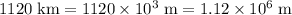Time required for the first part of this trip:

`\displaystyle (5.60 * 10^(5)\; \rm m)/(602\; \rm m\cdot s^(-1)) \approx 930\; \rm s`.

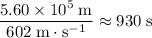Time required for the second part of this trip:

`\displaystyle (5.60 * 10^(5)\; \rm m)/(903\; \rm m\cdot s^(-1)) \approx 620\; \rm s`.

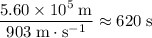The time required for the entire trip would be approximately
`930 + 620 = 1550\; \rm s`.

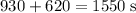Calculate the average speed of this plane:

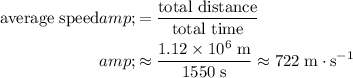`\begin{aligned} \text{average speed} &= \frac{\text{total distance}}{\text{total time}} \\ &\approx (1.12* 10^(6)\; \rm m)/(1550\; \rm s) \approx 722\; \rm m \cdot s^(-1)\end{aligned}`.