Question

The marks obtained by Sean and Zack in a test are 4x+6 and 3x+15 respectively. If Sean obtains at least 2 marks more than Zack, what is the minimum value of x?

Answer 1

The minimum value of x will be 11.

Explanation:

We are given that the marks obtained by Sean and Zack on a test are (4x + 6) and (3x + 15), respectively. Sean obtained at least two more marks than Zack, and we want to find the minimum value of x.

Since Sean obtained at least two more marks than Zack, we can write that:

`\displaystyle 4x + 6 \geq (3x + 15)+2`

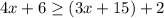
Solve for x:

`\displaystyle \begin{aligned} 4x + 6 & \geq 3x + 17 \\ \\ x + 6 & \geq 17 \\ \\ x &\geq 11\end{aligned}`

Hence, the value of x must be greater than or equal to 11.

Then the minimum value of x will be 11.