Question

Your friend says that the absolute value equation | 3x+8 |-9=-5 has no solution because the constant

on the right side of the equation is negative. Is your friend correct? Explain

Answer 1

Incorrect

Explanation:

We are given the equation:

`\displaystyle \large`

Add both sides by 9.

`\displaystyle \large \\ \displaystyle \large3x+8`

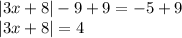
When we want to tell if the absolute equation has solutions or not, we have to simplify in this form first: or isolate the absolute sign.

`\displaystyle \large`

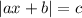
If c ≥ 0, the equation has solutions.

If c < 0, the equation does not have solutions.

Therefore, it does not always matter if the constant on right side is in negative because if there is a number on the left side then there is a chance that the equation has solutions.

From |3x+8| = 4 is equivalent |3x+8|-9=-5 and the right side is 4 which is positive.

Hence, the equation does have a solution!