Answer:
A. Solutions are: x = 2, y = 1.
B. Solutions are: x = 3, y = 2.
C.
1. Inconsistent
2. Inconsistent
3. Consistent
Explanation:
A. Solutions of each system of linear equations by substitution method:
Equation 1: 3x - 2y = 4
Equation 2: x = 2y
Step 1: Substitute x = 2y into the Equation 1:
3(2y) - 2y = 4
6y - 2y = 4
4y = 4
Step 2: Divide both sides of the equation by 4 to isolate y:
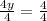
y = 1.
Step 3: For Equation 2, x = 2y, substitute y = 1 into the equation to solve for x:
x = 2y
x = 2(1)
x = 2
Therefore, the solutions are: x = 2, y = 1.
B. Find the solutions of each system of linear equations by elimination method:
Equation 1: 2x + y = 8
Equation 2: x + y = 5
Step 1: Multiply Equation 2 by 2:
2(x + y) = 5(2)
2x + 2y = 10
Step 2: Subtract Equation 1 from the equation derived from Step 1, 2x + 2y = 10:
2x + 2y = 10
- 2x + y = 8
y = 2
Step 3: Plug in y = 2 into Equation 1, 2x + y = 8 to solve for x:
2x + y = 8
2x + (2) = 8
Step 4: subtract both sides of the equation by 2 to isolate x:
2x + 2 - 2 = 8 - 2
2x = 6
Step 5: Divide both sides of the equation by 2 to solve for x:
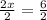
x = 3.
The solutions are: x = 3, y = 2.
C:
1. Inconsistent
2. Inconsistent
3. Consistent (infinitely many solutions)