Problem 1 is correct. You use the pythagorean theorem to find the hypotenuse.
==================================================
Problem 2 has the correct answer, but one part of the steps is a bit strange. I agree with the 132 ft/sec portion; however, I'm not sure why you wrote
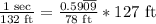
I would write it as

==================================================
For problem 3, we first need to convert the runner's speed from mph to feet per second.
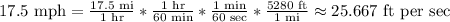
Since the runner needs to travel 90-12 = 78 ft, this means
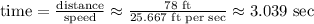
So the runner needs about 3.039 seconds. In problem 2, you calculated that it takes about 0.96 seconds for the ball to go from home to second base. The runner will not beat the throw. The ball gets where it needs to go well before the runner arrives there too.
-------------
The question is now: how much of a lead does the runner need in order to beat the throw?
Well the runner needs to get to second base in under 0.96 seconds.
Let's calculate the distance based on that, and based on the speed we calculated earlier above.
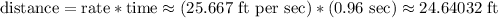
This is the distance the runner can travel if the runner only has 0.96 seconds. So the lead needed is 90-24.64032 = 65.35968 feet
This is probably not reasonable considering it's well over halfway (because 65.35968/90 = 0.726 = 72.6%). If the runner is leading over halfway, then the runner is probably already in the running motion and not being stationary.
As you can see, the runner is very unlikely to steal second base. Though of course such events do happen in real life. What may explain this is the reaction time of the catcher may add on just enough time for the runner to steal second base. For this problem however, we aren't considering the reaction time. Also, not all catchers can throw the ball at 90 mph which is quite fast. According to quick research, the MLB says the average catcher speed is about 81.8 mph. This slower throwing speed may account for why stealing second base isn't literally impossible, although it's still fairly difficult.