The series you had provided is generally the Maclaurin's series , and we want to prove the series , this series is very very much useful in calculus , especially when you have to substitute a function by it's series . So now let's start !
Consider the function f(x) as series of a polynomials of nth (n ≥ 1) degree as
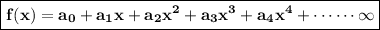
Now , at x = 0


Now , again consider the function that we assumed
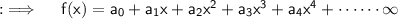
Differentiating both sides w.r.t.x will yield
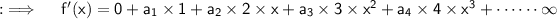
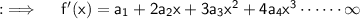
Now , put x = 0 ;
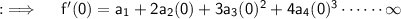
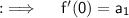
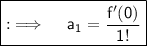
Now , consider ;
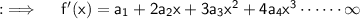
Differentiating both sides w.r.t.x now ;
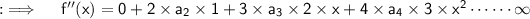
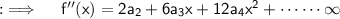
Now , putting x = 0 will yield ;
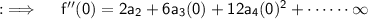
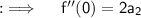
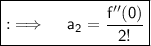
Now , similarly we can prove that ;
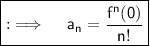
Now , as we had considered ;
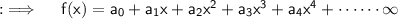
Now , putting the values we obtained above ;
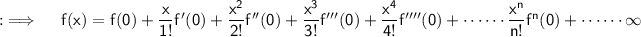
Hence , Proved