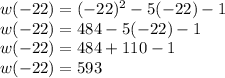Evaluating Composite Functions
Answer:
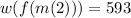
Explanation:
We can write how
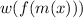 will be defined but that's too much work and it's only useful when we are evaluating
will be defined but that's too much work and it's only useful when we are evaluating
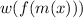 with many inputs.
with many inputs.
First let's solve for
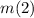 first. As you read through this answer, you'll get the idea of what I'm doing.
first. As you read through this answer, you'll get the idea of what I'm doing.
Given:
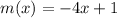
Solving for
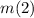 :
:
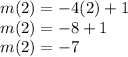
Now we can solve for
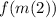 , since
, since
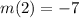 ,
,
 .
.
Given:
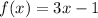
Solving for
 :
:

Now we are can solve for
 . By now you should get the idea why
. By now you should get the idea why
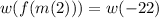 .
.
Given:

Solving for
 :
: