Question

Y=3x-11
y-3x=-13

Solving using systems of equations

Answer 1

Ø

Explanation:

These equations are parallel, meaning they have SIMILAR rate of changes [slopes]. To prove it, convert the second equation from Standard Form to Slope-Intercept Form:

`\displaystyle y - 3x = -13 \hookrightarrow y = 3x - 13 \\ \\ \left \{ {{y = 3x - 13} \atop {y = 3x - 11}} \right.`

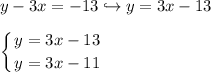
As you can see, both equations have a rate of change of 3, meaning we CANNOT obtain a solution here, therefore we have no solution.

I am joyous to assist you at any time.

Answer 2

Answer: There are no possible solutions because

If you were to plot these two equations on the graph you would notice they are parallel because both have the same slope (3x) but still have different intercepts. This means there are no possible solutions as in order to have a solution for x and y they need to intercept and the point of interception is the solution for x and y but that cannot happen in a system of equations that result in parallel lines ( they’ll never intercept)