Answer:
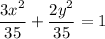
Explanation:
we want to figure out the ellipse equation which passes through (1,4) and (-3,2)
the standard form of ellipse equation is given by:
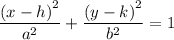
where:
- (h,k) is the centre
- a is the horizontal redius
- b is the vertical radius
since the centre of the equation is not mentioned, we'd assume it (0,0) therefore our equation will be:
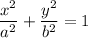
substituting the value of x and y from the point (1,4),we'd acquire:
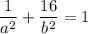
similarly using the point (-3,2), we'd obtain:
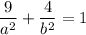
let 1/a² and 1/b² be q and p respectively and transform the equation:
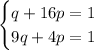
solving the system of linear equation will yield:
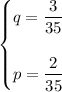
substitute back:
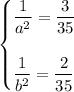
divide both equation by 1 which yields:
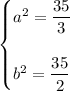
substitute the value of a² and b² in the ellipse equation , thus:
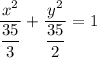
simplify complex fraction:
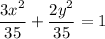
and we're done!
(refer the attachment as well)