Answer:
4
Explanation:
a and B are the roots of
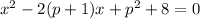
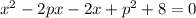
This look like a parabola since p will be a constant so let use a quadratic formula
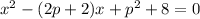
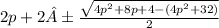
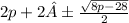
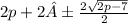
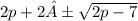
So the roots are
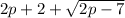
and
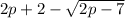
We know the distance between these two points are
2 so
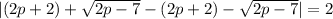



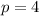
Let plug it in to see.


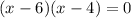
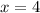
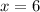
So they have a distance of 2.