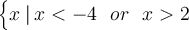Answer:
x
Explanation:
We are given the Inequality:
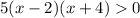
Since the expression is in factored form, no need to expand it.
First, let's understand Parabola. See the attachment below.
Since the Inequality above means that the equation, function or graph must be above x-axis.
That's because in the given Inequality, we are saying that the parabola y = 5(x-2)(x-4) is greater than y = 0 or basically x-axis.
See the attachment again - I shaded the region where the function is greater than y = 0.
The value of y keeps getting bigger and bigger when we keep substituting x < -4 or x > 2.
Hence, the answer is: