Answer:
x = 2
Explanation:
What is needed to solve this equation is a common denominator. With a common denominator, you can get rid of subtracted fractions.
First, factor the denominator on the left side of the equation:
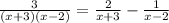
Then, create a common denominator on the right:
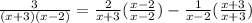
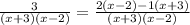
Put everything on one side:
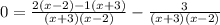
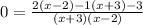
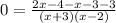
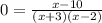
set each term equal to zero:
x - 10 = 0
x = 10
x + 3 = 0
x = -3
x - 2 = 0
x = 2 is the answer, since it is the only answer which is listed in the multiple choice question.