Question

Trying to simplify an equation, but it's apparently wrong.

So I'm solving a limit problem, where I try to see what happens as a function approaches x = 1. I just need to simplify an equation to solve that, which is what I'm stuck on right now.

The expression is
`(√(17-x)-4 )/(√(2-x)-1 )`

I first multiply the numerator and denominator by the denominator to get that ugly square root out of there. That gets me to
`((√(17-x)-4) * (√(2-x)+1) )/(2-x-1)`

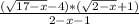
The denominator can be simplified to -x - 1.

I then plug 1 into the equation to find the limit I'm looking for.
`((√(17 - 1) - 4) * (√(1)+1) )/(-1 - 1)`

Doing basic math on both the numerator and denominator, I simplify this down to 0 / -2, which is just 0. However, this apparently is the wrong answer. Can anyone see if they can find if I made an error anywhere? Thanks!

Answer 1

Explanation:

Letting the variable x approach 1 will give us
`(0)/(0)`, an indeterminate result. In such a case, we can use L'Hopital's rule where

`\displaystyle \lim_(x \to c) (f(x))/(g(x)) = \lim_(x \to c) (f'(x))/(g'(x))`

Let
`f(x) = √(17 - x) - 4` and

`g(x) = √( 2 - x) - 1`

We can see that

`f'(x) = -(1)/(2)(17 - x)^{-(1)/(2)}`

and

`g'(x) = -(1)/(2)(2 - x)^{-(1)/(2)}`

Applying L'Hopital's rule, we get

`\displaystyle \lim_(x \to 1) (√(17 - x) - 4)/(√( 2 - x) - 1) = \lim_(x \to 1) \frac{-(1)/(2)(17 - x)^{-(1)/(2)}}{-(1)/(2)(2 - x)^{-(1)/(2)}}`

`\:\:\:\:\:\:\:\:= \displaystyle \lim_(x \to 1) \sqrt{(2 - x)/(17 - x)} =\sqrt{(1)/(16)} = (1)/(4)`

Therefore, as
`x \rightarrow 1,` the given expression approaches
`(1)/(4)`.