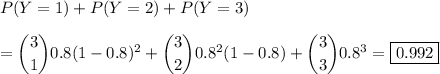Question

Pls help me solve this question . Thank you

Answer 1

(i) The probability of failing to qualify on the first two jumps and succeeding on the third is

(1 - 0.8) (1 - 0.8) 0.8 = 0.032

In other words, if X is the random variable representing the first qualifying jump, then X is geometrically distributed and the probability of qualifying for the final round on exactly the n-th jump is

`P(X=n) = (1-0.8)^(n-1)*0.8`

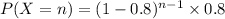
(ii) In order to qualify for the final round, David has to succeed on at least one jump. Let Y be the random variable representing how many successful jumps are made. Then Y is binomially distributed with

`P(Y = n) = \dbinom3n 0.8^n*(1-0.8)^(3-n)`

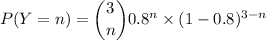
The probability of succeeding at least once is

`P(Y=1) + P(Y=2) + P(Y=3) \\\\ = \dbinom310.8(1-0.8)^2 + \dbinom320.8^2(1-0.8) + \dbinom33 0.8^3 = \boxed{0.992}`