If you take the point on the bridge directly beneath the lowest point on the cable to be the origin, then the parabola has equation
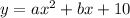
300 ft to either side of the origin, the parabola reaches a value of y = 90, so
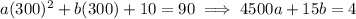
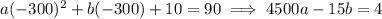
Adding these together eliminates b and lets you solve for a :
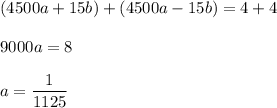
Solving for b gives
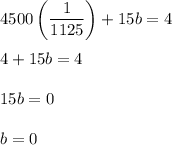
So the parabola's equation is
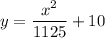
150 ft away from the origin, the cable is at a height y of
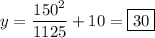
ft above the bridge.