Question

Three tanks are filled with a dye solution. Tanks A and B initially contains 20 hg of dye and tank C is initially pure water. A solution that contains 3 hg/L of dye is pumped into tank A at a rate of 50 L/hr. The solution in tank A flows out to tank B at a rate of 40 L/hr and out an exhaust spout at a rate of 20 L/hr. The solution in tank B into tank A at a rate of 10 L/hr, into tank C at a rate of 30 L/hr, and out an exhaust spout at a rate of 10 L/hr. The solution in tank C flows into tank B at a rate of 10 L/hr and out an exhaust spout at a rate of 20 L/hr. If tank A holds 200 L, tank B holds 100 L, and tank C holds 100 L, set up a system to determine the amount of dye in each tank at a given time t.

Answer 1

Let A(t), B(t), and C(t) denote the amounts (in hg) of dye in tanks A, B, and C, respectively.

Both A and B start with 20 hg of dye, so A(0) = B(0) = 20. C starts off containing only pure water, so C(0) = 0.

The amount of dye in a given tank changes at a net rate equal to the difference between how much dye flows in and how much flows out.

• Tank A:

•• Dye flows in from an independent source at a rate of

(3 hg/L) (50 L/hr) = 3/50 hg/hr

That is,

(concentration of dye) (flow rate) = rate of change in amount of dye

and the concentration is equal to the amount of dye per unit volume.

Dye also flows in from tank B at a rate of

(B(t)/100 hg/L) (10 L/hr) = B(t)/10 hg/hr

•• Dye flows out of A into B at a rate of

(A(t)/200 hg/L) (40 L/hr) = A(t)/5 hg/hr

and out the exhaust spout at a rate of

(A(t)/200 hg/L) (20 L/hr) = A(t)/10 hg/hr

•• Then the net rate dA/dt is

`(\mathrm dA)/(\mathrm dt) = \frac3{50}+(B(t)-3A(t))/(10)`

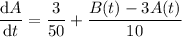
• Tank B:

•• Dye flows in from A at a rate of

(A(t)/200 hg/L) (40 L/hr) = A(t)/5 hg/hr

and from C at a rate of

(C(t)/100 hg/L) (10 L/hr) = C(t)/10 hg/hr

•• Dye flows out into A at a rate of

(B(t)/100 hg/L) (10 L/hr) = B(t)/10 hg/hr,

out into C at a rate of

(B(t)/100 hg/L) (30 L/hr) = 3B(t)/10 hg/hr,

and out the exhaust spout at a rate of

(B(t)/100 hg/L) (10 L/hr) = B(t)/10 hg/hr

•• The net rate dB/dt is then

`(\mathrm dB)/(\mathrm dt) = (2A(t)+C(t)-5B(t))/(10)`

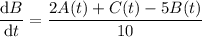
• Tank C:

•• Dye flows from B at a rate of

(B(t)/100 hg/L) (30 L/hr) = 3B(t)/10 hg/hr

•• Dye flows out into B at a rate of

(C(t)/100 hg/L) (10 L/hr) = C(t)/10 hg/hr

and out the exhaust spout at a rate of

(C(t)/100 hg/L) (20 L/hr) = C(t)/5 hg/hr

•• The net rate dC/dt is then

`(\mathrm dC)/(\mathrm dt) = (3B(t)-3C(t))/(10)`

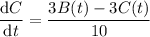
Condensed into a matrix equation, the system of ODEs can be expressed as

`(\mathrm d\mathbf X)/(\mathrm dt) = \frac1{10}\begin{pmatrix}-3&1&0\\2&-5&1\\0&3&-3\end{pmatrix}\mathbf X + \frac1{50}\begin{pmatrix}3\\0\\0\end{pmatrix}`

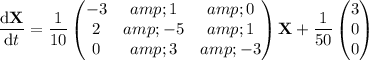
where

`\mathbf X = \begin{pmatrix}A(t)\\B(t)\\C(t)\end{pmatrix}`

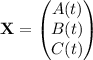
and with initial condition

`\mathbf X(0) = \begin{pmatrix}20\\20\\0\end{pmatrix}`

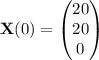
Just for fun, here's a plot of the solution to this system for the first 50 hours after the pumps are started: