Notice that
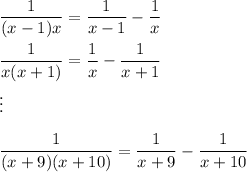
That is, the n-th term (where n = -1, 0, 1, …, 9) in the sum on the left side has a partial fraction decomposition of
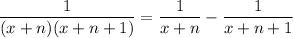
and in the sum, some adjacent terms will cancel and leave you with

Now solve for x, bearing in mind that we cannot have x = 0, -1, -2, …, -10 :

Combine the fractions on the left side:
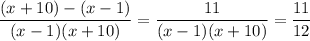
Then we must have

so that either x = 2 or x = -11.