Question

What is the equation of the line that passes through
(-2, 4) and (2, 7)?

Answer 1

`y=(3)/(4)x+(11)/(2)`

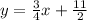
Explanation:

Hi there!

We want to find the equation of the line that passes through (-2, 4) and (2, 7).

The most common way to write the equation of the line is in slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept.

First, let's find the slope of the line.

The slope, calculated from two points is given as the formula
`(y_2-y_1)/(x_2-x_1)`, where
`(x_1, y_1)` and
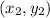`(x_2, y_2)` are points.

We have two points, which is needed to find the slope, but let's label their values to avoid confusion.

`x_1=-2\\y_1=4\\x_2=2\\y_2=7`

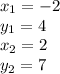
Now substitute those values into the formula.

m=
`(y_2-y_1)/(x_2-x_1)`

m=
`(7-4)/(2--2)`

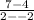
Simplify

m=
`(7-4)/(2+2)`

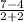
m=
`(3)/(4)`

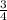
So the slope of the line is
`(3)/(4)`.

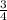Substitute that value as m in y=mx+b

y=
`(3)/(4)x+b`

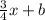
Now we need to find b

As the equation passes through both (-2, 4) and (2, 7), we can substitute the values of either one of them in the equation to solve for b

Taking (-2, 4) for example,

Substitute -2 as x and 4 as y:

4=
`(3)/(4)(-2)+b`

Multiply

4=
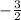`-(3)/(2)`+b

Add -3/2 to both sides

`(11)/(2) = b`

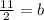
Substitute that value into the equation

y=
`(3)/(4)x+(11)/(2)`

Hope this helps!