Final Answer:
The future value (FV) of Sutton's deposit of $7500 into an account with a 6.24% annual interest rate compounded monthly after 7 years is approximately $11,407.88.
Step-by-step explanation:
To calculate the future value, we use the compound interest formula:
![\[FV = P \left(1 + (r)/(n)\right)^(nt)\]](https://img.qammunity.org/2022/formulas/mathematics/college/sbhtlfy9c83ep7qfb4f6gwqhlmi4nb5rvj.png)
Where:
- FV is the future value of the investment/loan.
- P is the principal amount (initial deposit or loan amount).
- r is the annual interest rate (as a decimal).
- n is the number of times that interest is compounded per unit
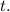
- t is the time the money is invested or borrowed for in years.
In this case:
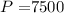
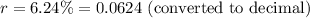
 (compounded monthly)
(compounded monthly)
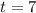 years
years
Substitute these values into the formula:
![\[FV = 7500 \left(1 + (0.0624)/(12)\right)^((12 * 7))\]](https://img.qammunity.org/2022/formulas/mathematics/college/ehk6r4hufrpmjjve7ljc0bmgmh5shm34zg.png)
Calculate the expression:
![\[FV \approx 7500 \left(1 + 0.0052\right)^(84)\]](https://img.qammunity.org/2022/formulas/mathematics/college/qqv6nhyh8o28rdpgbp6pk3fstye3ex6cpp.png)
![\[FV \approx 7500 * 1.5017962\]](https://img.qammunity.org/2022/formulas/mathematics/college/3jcax0k1q06f61jqyjkdhdgf68q1rk9luv.png)
![\[FV \approx 11,407.88\]](https://img.qammunity.org/2022/formulas/mathematics/college/78haoi5h2qf6lmlt9ssp8lgyqxazqt3xbn.png)
Therefore, after 7 years, Sutton's deposit will grow to approximately $11,407.88. This calculation takes into account the compounded interest, resulting in the final future value of the deposit.