Question

What is the sum of the geometric series, rounded to the nearest whole number? 16 E n-1

6(1/4)^n A=2, B=3, c=4 d=6

What's the correct answer please

Answer 1

The infinite sum is (first term) divided by (1 minus the common ratio). The first term is 6(1/4) = 3/2; the common ratio is 1/4:

`S=((3)/(2) )/(1-(1)/(4) ) =((3)/(2) )/((3)/(4) ) =((3)/(2) )*((4)/(3) )=2`

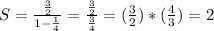
The terms after n=16 are tiny and will certainly bring the sum down only a tiny bit.

So to the nearest whole number the sum of the finite geometric series is 2.