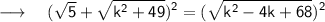Step-by-step explanation:
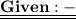

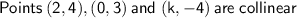
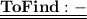
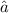
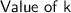


Let us consider these points on a line AC such that point B lies in between points A and C as these lines are collinear -
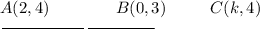
If lines are collinear then,


We will find distance between points by distance formula-
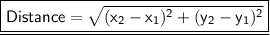

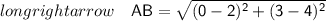
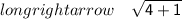
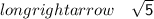

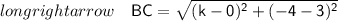
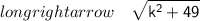

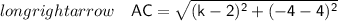
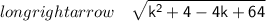

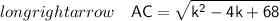

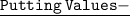
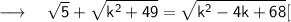
Squaring Both Sides-