Question

Please share whatever knowledge you have for these 2 mathematical topics:

1. Direct and Indirect Proportion/Variations
2. Indices and Standard Form

I'll really appreciate if you take your precious time out. If I had any further queries on your answer I'll ask through comments, hope you'll reply. Thank you! ​​

Answer 1

Explanation:

this soln. for your first question

Step 1

(Forming an expression in terms of x, y and k

it says y is directly proportional to cube root of z

that is

`y = k( {x}^{ (1)/(3) } ) \\ or \\ y = k (\sqrt[3]{x} )`

Step 2

(using the example based on the equation to find constant k)

the questions states that the value of y js 18 when x is 27

putting these values in the above expression

`18 = k( {27}^{ (1)/(3) } )`

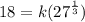
cube root of 27 is 3 as we get 27 when 3 is multiplies thrice to itself

18 = k × 3

k = 6

Now, since we have the value of k, let's form the final expression in terms of y and x

Step 3

(forming the final expression in terms of x and y)

remember? earlier we had an expression like

`y = k( {x}^{ (1)/(3) } )`

now, we'll just replace k with its value obtained in Step 2

`y = 6( {x}^{ (1)/(3) } )`

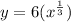
Thus, we have an expression in terms of y and x that satisfies the greens of the question.

For part (b) you have to find the value if y at x = 125

so simply put x = 125 in thus expression and then solve for y you'll get the answer.

now, question 2

(a)

it says find the value of

`{3}^( - 2)`

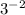
if we have a base with negative exponent it means we gotta find the value of it's reciprocal raised to the positive exponent

reciprocal of 3 = 1/ 3

`{3}^( -2 ) ={ ( (1)/(3) )}^(2)`

which is equal to 1/ 9 so that's your answer :}

(b)

next we have

`{( (1)/(16))}^{ (1)/(2) }`

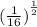
if we have the exponent in fractional form with numerator as 1, that is reciprocal of a proper exponent, we simply have to find out the root

like here ithe exponent is 1/ 2 so well find its square root

= 1/ 4

Next question

p = 8 × 10⁹

q = 4 × 10⁷

(a) p × q

Step 1

write the given values of p and q in the expression

(8 × 10⁹) × (4 × 10⁷)

Step 2

pull all "10 raised to the power something" together and solve for the rest

8 × 4 × (10⁹ × 10⁷)

32 × (10⁹ × 10⁷)

Step 3

add the exponents of "10 raised to the power something" while the base remains the same

`32 * 10 {}^(9 + 7)`

`= 32 * 10 {}^(16)`

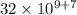
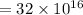
so, this is the answer and if it's not then please inform

(b) q ÷ p

follow the same steps as in option (a) but wait after your done with Step 2

Step 1

`\frac{4 * {10}^(7) }{8 * {10}^(9) }`

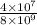
Step 2

`(4)/(8) * \frac{10 {}^(7) }{ {10}^(9) }`

`(1)/(2) * \frac{10 {}^(7) }{ {10}^(9) }`

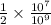
Step 3

subtract the exponents of "10 raised to the power something" while the base remains the same

`(1)/(2) * {10}^(7 - 9)`

`(1)/(2) * {10}^( - 2)`

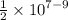
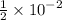
1/ 2 can also be written as 0. 5

`0.5 * {10}^( - 2)`

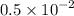
(c) p + q

Step 1 remains the same

Step 1

8 × 10⁹ + 4 × 10⁷

Step 2

divide and multiply the expression with 4 × 10⁷

(why?)

this procedure is followed when you take out a variable

that is common in a summation expression .

so for this we'll multiply and divide the expression with the GCD of the two variables without exponents and 10 raised to the power of that exponent which is the smallest

here GCD of 4 and 8 is 4

and smallest exponent with base 10 is 7

so we multiply and divide the expression with 4 × 10⁷

`4 * 10 {}^(7) ( \frac{ 8 * {10}^(9) + 4 * {10}^(7) }{4 * {10}^(7) } )`

and remember! don't cancel them out

we can write it as

`4 * 10 {}^(7) ( \frac{ 8 * {10}^(9) }{4 * {10}^(7) } + \frac{ 4 * {10}^(7)}{ 4 * {10}^(7)} )`

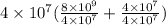
now for division carry out the same steps as you did in part (b)

=> 4 × 10⁷ ( 2 × 10² + 1)

10² = 100

2 × 10² = 200

=> 4 × 10⁷ ( 200 + 1 )

=> 4 × 10⁷ × 201

=> 804 × 10⁷

this must be the answer

you must be wondering about why we reduced 10² to 100 so for this remember that if you have any two quantities in summation that can be added EASILY if you write them in standard form, then there's no one stopping you! go ahead!