Question

PLEASE HELP!!
Algebra II

Answer 1

f(-8) = -512, f(8) = 2

Explanation:

Substitute x = -8 and 8 into the function, taking into account the rules of the function.

For x = -8, x < 0 so the value is equal to the cube of -8, which is -512.

For x = 8, x > 0 so the value is equal to the cube root of 8, which is 2.

Answer 2

Hey there! :)

We are given the piecewise function:

`\displaystyle \large{f(x) = \begin{cases} {x}^(3) \: \: (x < 0) \\ \sqrt[3]{x} \: \: (x > 0) \end{cases}}`

To evaluate the value of function at x = -8 and x = 8, we know that -8 is less than 0 and 8 is greater than 0.

Therefore, if we want to evaluate the value of function at x = -8; we use the x^3 since it's given x < 0 for the function and for x = 8; we use the cube root of x since it's given x > 0.

Evaluate x = -8

From the piecewise function:

`\displaystyle \large{f(x) = \begin{cases} {x}^(3) \: \: (x < 0) \\ \sqrt[3]{x} \: \: (x > 0) \end{cases}}`

Since -8 is less than 0, we use x^3.

`\displaystyle \large{f( - 8) = {( - 8)}^(3) } \\ \displaystyle \large{f( - 8) = - 512}`

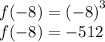
Evaluate x = 8

From the piecewise function, since 8 is greater than 0, we use the cube root of x.

`\displaystyle \large{f(8) = \sqrt[3]{8} }`

To evaluate the cube root, first we prime-factor the number.

`\displaystyle \large{f(8) = \sqrt[3]{2 \cdot 2 \cdot 2} }`

Since it's a cube root, we pull three 2's out of the cube root and write only one 2.

`\displaystyle \large{f(8) =2}`

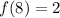
Answer

• f(-8) = -512
• f(8) = 2

Let me know if you have any questions!