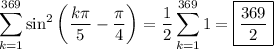Question

I don’t know how to do part a

Answer 1

(a) The claim is made for all positive integers n, so we start at n = 1. We have

`\displaystyle \sin(x) \sum_(k=1)^1 \sin(2kx) = \sin(x) \sin(2x) = \sin(1x) \sin((1+1)x)`

so the claim is true for the base case.

Suppose the claim is true for n = m, so that

`\displaystyle \sin(x) \sum_(k=1)^m \sin(2kx) = \sin(mx) \sin((m+1)x)`

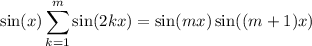
We want to use this to establish the identity for n = m + 1. That is, we want to prove that

`\displaystyle \sin(x) \sum_(k=1)^(m+1) \sin(2kx) = \sin((m+1)x) \sin((m+2)x)`

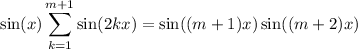
Working with the left side, we remove the last term from the sum and we have

`\displaystyle \sin(x) \sum_(k=1)^(m+1) \sin(2kx) = \sin(x) \sum_(k=1)^m \sin(2kx) + \sin(x) \sin(2(m+1)x) \\\\\\ = \sin(mx) \sin((m+1)x) + \sin(x) \sin(2(m+1))x`

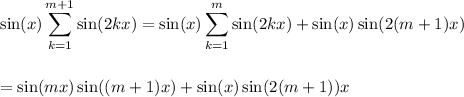
Recall the angle sum identities:

`\sin(x + y) = \sin(x) \cos(y) + \cos(x) \sin(y)`

`\sin(x - y) = \sin(x) \cos(y) - \cos(x) \sin(y)`

`\cos(x + y) = \cos(x) \cos(y) - \sin(x) \sin(y)`

`\cos(x - y) = \cos(x) \cos(y) + \sin(x) \sin(y)`

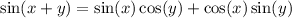
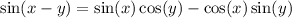
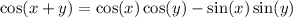
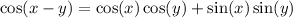
Then

`\sin(2(m+1)x) = 2 \sin((m+1)x) \cos((m+1)x)`

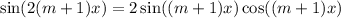
so we can remove a factor of sin((m + 1) x) :

`\displaystyle \sin(x) \sum_(k=1)^(m+1) \sin(2kx) = \sin((m+1)x) \bigg(\sin(mx) + 2 \sin(x) \cos((m+1)x)\bigg)`

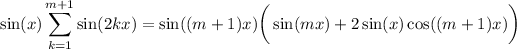
and we also have

`2 \sin(x) \cos((m+1)x) = \sin(x+(m+1)x) + \sin(x - (m+1)x) \\\\ = \sin((m+2)x) + \sin(-mx) \\\\ = \sin((m+2)x) - \sin(mx)`

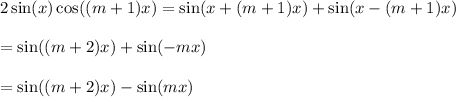
Then the sin(mx) terms cancel, and we're left with what we wanted:

`\displaystyle \sin(x) \sum_(k=1)^(m+1) \sin(2kx) = \sin((m+1)x) \sin((m+2)x)`

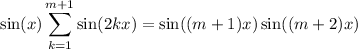
and the induction proof is complete.

(b) From the identities mentioned earlier, one has

`\sin\left(x - \frac\pi4\right) = \sin(x) \cos\left(\frac\pi4\right) - \cos(x) \sin\left(\frac\pi4\right) \\\\ = (\sin(x) - \cos(x))/(\sqrt2)`

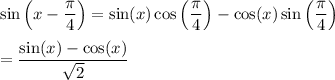
Then

`\sin^2\left(x - \frac\pi4\right) = \frac{(\sin(x) - \cos(x))^2}2 \\\\ = \frac{\sin^2(x) - 2 \sin(x) \cos(x) + \cos^2(x)}2 \\\\ = \frac{1 - \sin(2x)}2`

We can then rewrite the sum as

`\displaystyle \sum_(k=1)^(369) \sin^2\left(\frac{k\pi}5 - \frac\pi4\right) = \frac12 \sum_(k=1)^(369) \left(1 - \sin\left(\frac{2k\pi}5\right)\right) \\\\ = \frac12 \sum_(k=1)^(369) 1 - \frac12 \sum_(k=1)^(369) \sin\left(\frac{2k\pi}5\right)`

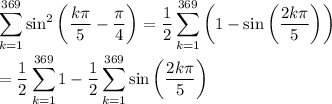
Recall that

`\displaystyle \sum_(k=1)^n 1 = 1 + 1 + \cdots + 1 = n`

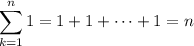
For the sum involving sine, let x = π/5. Then using the result from part (a),

`\displaystyle \sin\left(\frac\pi5\right) \sum_(k=1)^(369) \sin\left(\frac{2k\pi}5\right) = \sin\left(\frac{369\pi}5\right) \sin\left(\frac{370\pi}5\right)`

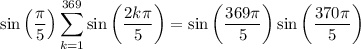
and this sum vanishes, since sin(370π/5) = sin(74π) = 0.

It follows that

`\displaystyle \sum_(k=1)^(369) \sin^2\left(\frac{k\pi}5 - \frac\pi4\right) = \frac12 \sum_(k=1)^(369) 1 = \boxed{\frac{369}2}`