
Given :-
- The sum of 3 consecutive even number is 144
- The lowest even number as 4x - 2
To Find :-
- We have to find the highest consecutive number.
Let's Begin :-
Here ,we have
- The sum of three consecutive even numbers is 144
- [ Consecutive even numbers are the sequence of numbers that differ by 2 or that are divisible by 2 ]
- The lowest even number is 4x - 2
Let the three consecutive number be
(4x - 2) , 4x , ( 4x + 2)
According to the question,
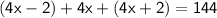
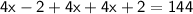
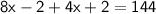
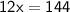
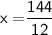
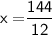
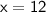
Thus, The value of x is 12
Therefore,
The three consecutive even numbers are
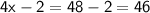

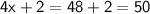
Hence, The highest consecutive even number is 50 .