Question

HELP !! Answer the questions shown

Answer 1

For a function to be continuous at an x-value of -3 you need to make sure two things line up:

First, we need to show that the limit from the left equals the limit from the right.

`\lim_(x \to -3^(-)) f(x) = \lim_(x \to -3^(+)) f(x)`

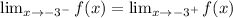
Second, we need to show that this limit equals the functions value.

`\lim_(x \to -3) f(x) = f(-3)`

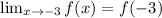
The left hand limit involves the first piece, f(x) = x^2 - 9:

`\begin{aligned} \lim_(x \to -3^(-)) f(x) &= \lim_(x \to -3^(-)) (x^2-9)\\[0.5em]&= (-3)^2-9\\[0.5em]&= 0\endaligned}`

The right hand limit invovles the second piece, f(x) = 0:

`\begin{aligned} \lim_(x \to -3^(+)) f(x) &= \lim_(x \to -3^(+)) (0)\\[0.5em]&= 0\endaligned}`

Since the two one-sided limits do match, we can just say:

`\lim_(x \to -3) f(x) = 0`

(no one-sided pieces needed now)

So that was step #1, to make sure the limit exists. Next we need to make sure the limit is headed to the same place where the functions. Since we're using x=-3, we'll use the top piece of the function because x=-3 fits with that piece ( x ≤ -3 ).

`f(-3) = (-3)^2-9 = 0`

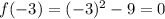
From this, we know that
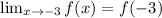`\lim_(x \to -3) f(x) = f(-3)`, so the function is continuous at -3. (We also know parabolas and lines are continuous in general, so we only needed to check where the two pieces came together at x = -3.)