Question

Is the function continuous at x = -17

Answer 1

For a function to be continuous at an x-value, say -17, you need to make sure two things line up:

The limit from the left equals the limit from the right.

`\lim_(x \to -17^(-)) f(x) = \lim_(x \to -17^(+)) f(x)`

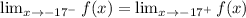
This limit equals the functions value.

`\lim_(x \to -17) f(x) = f(-17)`

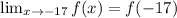
The left hand limit involves the first piece, f(x) = 20x + 1:

`\begin{aligned} \lim_(x \to -17^(-)) f(x) &= \lim_(x \to -17^(-)) (20x+1)\\[0.5em]&= 20(-17)+1\\[0.5em]&= -339\endaligned}`

The right hand limit invovles the second piece, f(x) = -10x^2:

`\begin{aligned} \lim_(x \to -17^(+)) f(x) &= \lim_(x \to -17^(+)) (-10x^2)\\[0.5em]&= -10\cdot (-17)^2\\[0.5em]&= -2890\endaligned}`

Since the two one-sided limits don't match, the function is not continuous at x=-17.