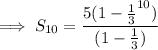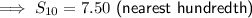Question

Evaluate geometric series

Answer 1

7.50 (nearest hundredth)

Explanation:

General form of geometric progression:
`a_n=ar^(n-1)`

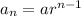
(where
`a` is the initial term and
`r` is the common ratio)

Given progression:

`5\left(\frac13\right)^(n-1)`

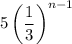
Therefore:

• 
  `a=5`
• 
  `r=\frac13`

Sum of a geometric series:

`S_n=(a(1-r^n))/((1-r))`

Substituting a = 5, r = 1/3 and n = 10 to find the sum to n = 10:

`\implies S_(10)=(5(1-\frac13^(10)))/((1-\frac13))`

`\implies S_(10)=7.499873987...`

`\implies S_(10)=7.50 \textsf{ (nearest hundredth)}`