Question

12. Find all x- and y-intercepts, state the multiplicity of each zero and tell if the graph crosses or

bounces, and state the end behavior Then graph each polynomial by hand,
P(x)=x^2(x-3)^2(x+2)


P(x)=x^4-4x^2

Answer 1

Explanation:

12a. To

find x intercepts, set each factor equal to zero

`{x}^(2) = 0`

`x = 0`

`(x - 3) {}^(2) = 0`

`x = 3`

`x + 2 = 0`

`x = - 2`

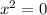
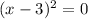
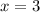
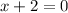
So the x intercepts are( 0,-2,3.)

The multiplicity of 0 and 3 is 2,

The multiplicity of -2 is 1.

The y intercepts are

`0 {}^(2) (0 - 3) {}^(2) (0 + 2) = 0`

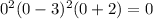
The y intercept is 0.

End Behavior: Since this is a positve 5th root function, as x increases, f(x) increases while as x decreases, f(x) decreases.

The First picture shows the graph of the function. Notice ried the zeroes that have a multiplicity of 2 have a parabolic reflection after thre function reaches their zero.

The zero that have a multiplicity of 1 have just passes through the graph.

12b. We have

`{x}^(4) - 4 {x}^(2)`

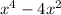
We can easily find y intercept, which is 0.

To find x intercept,

Factor

`{x}^(2) ( {x}^(2) - 4)`

`{x}^(2) (x + 2)(x - 2) = 0`

`x = 0`

`x = 2`

`x = - 2`

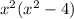
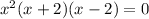
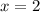
So the x intercepts are (0,2,-2).

The multiplicity of 0 is 2 while 2 and -2 is 1.

End Behavior: Since this is a positve quartic function, as x increases or decreases , f(x) increases

Look at the second graph,

Answer 2

`P(x)=x^2(x-3)^2(x+2)`

y-intercept is when x = 0:

`\implies P(0)=0^2(0-3)^2(0+2)=0`

Therefore, y-intercept is at (0, 0)

x-intercept(s) is when P(x) = 0

`\implies x^2(x-3)^2(x+2)=0`

`\implies x^2=0\implies x=0`

`\implies (x-3)^2=0\implies x=3`

`\implies (x+2)=0\implies x=-2`

Therefore, x-intercepts are:

• (0, 0) with multiplicity 2 → bounces
• (3, 0) with multiplicity 2 → bounces
• (-2, 0) with multiplicity 1 → crosses x-axis

End-behavior:

As the lead coefficient is positive and the lead degree is odd,

`P(x) \rightarrow - \infty \textsf{ as }x\rightarrow - \infty`

`P(x) \rightarrow + \infty \textsf{ as }x\rightarrow +\infty`

-------------------------------------------------------------------------------

`P(x)=x^4-4x^2`

y-intercept is when x = 0:

`\implies P(0)=(0)^4-4(0)^2=0`

Therefore, y-intercept is at (0, 0)

x-intercept(s) is when P(x) = 0

`\implies x^4-4x^2=0`

`\implies x^2(x^2-4)=0`

`\implies x^2(x-2)(x+2)=0`

`\implies x^2=0 \implies x=0`

`\implies (x-2)=0 \implies x=2`

`\implies (x+2)=0 \implies x=-2`

Therefore, x-intercepts are:

• (0, 0) with multiplicity 1 → crosses x-axis
• (2, 0) with multiplicity 1 → crosses x-axis
• (-2, 0) with multiplicity 1 → crosses x-axis

End-behavior:

As the lead coefficient is positive and the lead degree is even,

`P(x) \rightarrow + \infty \textsf{ as }x\rightarrow - \infty`

`P(x) \rightarrow + \infty \textsf{ as }x\rightarrow +\infty`