2 Answers

Tomwalsham · Answer 1 · 2023-02-27T23:10:11+0000

Answer:

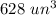
$628 \text{ }un^3$

Skills needed: Cone Formulas

Explanation:

1) The figure here is known as a cone (like an ice cream cone perhaps). The cone has special formulas, one being the one for volume.

- Volume is the total amount of 3d space taken up by a figure. It takes into account all 3 dimensions and is in cubic units.

---> The formula for the volume of a cone is:

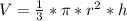
$V=\frac{1}3*\pi*r^2*h$

V=volume

$\pi = 3.14$ (FOR THIS PROBLEM PI IS 3.14 (AS IT IS STATED) -- In other cases, PI may be a different value based on what the problem says)

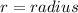r=radius , which is the radius of the circular base (In this case, that would be 10 units).

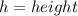h=height , a line from the center of the base to the top vertex (6 units)

--->
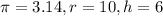$\pi=3.14, r=10, h=6$ --> We can easily solve for volume by plugging it in.

2) Solving it out:

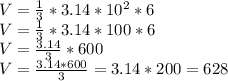
$V=\frac{1}3*3.14*10^2*6 \\ V=\frac{1}3*3.14*100*6 \\ V=\frac{3.14}3*600 \\ V=\frac{3.14*600}3=3.14*200=628$

The above is just me using order of operations and evaluating out for the volume. We end up with the result of 628.

---> If you are allowed to use a calculator, it can go a lot quicker.

Please log in or register to add a comment.