There are two ways to approach this.
The first is to just check with equation works with both points by plugging in x=6 and seeing if you get y=3, from the point (6,3), and then repeating that process with (4,1).
Checking (6,3) on y = -1x+5:
y = -1(6)+5 = -1 -> no good.
Checking (6,3) on y = x-3:
y = 6-3 = 3 -> check
Checking (6,3) on y = x+5:
y = 6+5 = 11 -> no good.
Checking (6,3) on y = -1x+3:
y = -1(6)+3 = -3 -> no good.
So that shows only y = 1x - 3 works, but you should still double check it works for (4,1).
The second option is to construct the equation, which is good to know, in case you don't have a list of equations to check.
For this, you need to calculate the slope, using
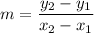 , and then use that slope to find the y-intercept, (0,b).
, and then use that slope to find the y-intercept, (0,b).
Step 1: slope
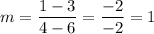
Step 2: find y-intercept
Start by setting up the slope-intercept form with the slope we just found and then plug in one of the points:
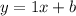 , which becomes
, which becomes
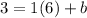 using (6,3).
using (6,3).
Solving this for b, you find b=-3.
Step 3: put it all together:
m = 1 and b = -1 gives you
y = 1x -3
Both ways work and are valid. Context will indicate which one is best.