Question

Find all real solutions Tan pi/3 x-3=0

Answer 1

Explanation:

If the question is like this,

`\tan( (\pi)/(3)x - 3 ) = 0`

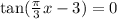
We take the arc tan of both sides.

`\tan( - 1) ( \tan( (\pi)/(3)x - 3 ) = \tan {}^( - 1) ( {}^( )0 )`

`(\pi)/(3) x - 3 = 0`

`(\pi)/(3) x = 3`

`= (9)/(\pi)`

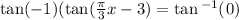
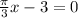
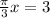
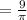
Since the period of a tan function, is pi, we divide pi by pi/3 since pi/3is the coeffeicent of the x variable

`(\pi)/( (\pi)/(3) ) = 3`

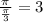
So the answer is

`(9)/(\pi) + 3n`

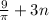
If this the question,

`\tan( (\pi)/(3) x) = 3`

`(\pi)/(3) x = 1.249`

`x = (3.747)/(\pi)`

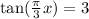
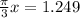
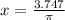
The period is once again 3 so we have

`(3.747)/(\pi) + 3n`

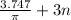
where n is a interger.