Question

A miniature quadcopter is located at x = -2.25 m and y, - 5.70 matt - 0 and moves with an average velocity having components Vv, x - 2.70 m/s and very - -2.50 m/s. What are the x-coordinate and

y-coordinate (in m) of the quadcopter's position at t= 1.60 ?

(a) x-coordinate
B y-coordinate

Answer 1

Recall that average velocity is equal to change in position over a given time interval,

`\vec v_(\rm ave) = (\Delta \vec r)/(\Delta t)`

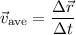
so that the x-component of
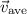`\vec v_(\rm ave)` is

`(x_2 - (-2.25\,\mathrm m))/(1.60\,\mathrm s) = 2.70(\rm m)/(\rm s)`

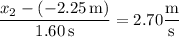
and its y-component is

`(y_2 - 5.70\,\mathrm m)/(1.60\,\mathrm s) = -2.50(\rm m)/(\rm s)`

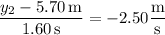
Solve for
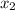`x_2` and
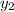`y_2`, which are the x- and y-components of the copter's position vector after t = 1.60 s.

`x_2 = -2.25\,\mathrm m + \left(2.70(\rm m)/(\rm s)\right)(1.60\,\mathrm s) \implies \boxed{x_2 = 2.07\,\mathrm m}`

`y_2 = 5.70\,\mathrm m + \left(-2.50(\rm m)/(\rm s)\right)(1.60\,\mathrm s) \implies \boxed{y_2 = 1.70\,\mathrm m}`

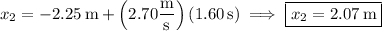
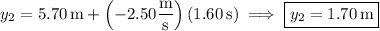
Note that I'm reading the given details as

`x_1 = -2.25\,\mathrm m \\\\ y_1 = -5.70\,\mathrm m \\\\ v_x = 2.70(\rm m)/(\rm s)\\\\ v_y=-2.50(\rm m)/(\rm s)`

so if any of these are incorrect, you should make the appropriate adjustments to the work above.