
Given :-
- Mary needs 50 ft of fence to protect her rectangular garden from squirrel
- The length of the garden is 8 ft more than the width
To Find :-
- We have to find the length and breath of the rectangular garden
Let's Begin :-
Mary needs 50ft of fence to protect her rectangular garden from squirrel
Therefore,
We can conclude that
The perimeter of the rectangular garden
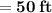
We know that,
Perimeter of the rectangle
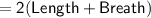
- Here, we have
- Length of the garden that is 8ft more than the width
Let assume the width of the garden be x
According to the question
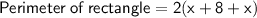
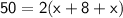
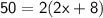
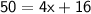
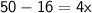
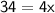

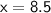
Thus, The breath of the garden is 8.5 ft
Therefore,
The length of the garden

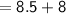
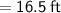
Hence, The length and breath of the rectangle are 8.5ft and 16.5ft .