Answer:
see below
Explanation:
we want to prove the following using mathematical induction
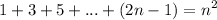
keep in mind that Mathematical Induction is a special way of proving things. It has only 2 steps:
- Show it is true for the first one
- Show that if any one is true then the next one is true
In fact,if you know about Domino effect . it will be easier to understand because That is how Mathematical Induction works! however let our topic back to the question. Showing the step is easy since we just need to prove the first one i.e n=1 . the second step is bit tricky so we'll handle it later,just a bit information the second step is all about assumption. it'll be required later
Step-1:Show it is true for the first one
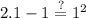
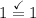
Step-2:Show that if any one is true then the next one is true
so assuming it true that n=k.we'd obtain
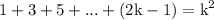
now let n=k+1 therefore we acquire:
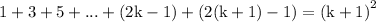
simplify which yields:
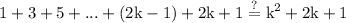
as I mentioned it's all about assumption therefore
 Thus,
Thus,
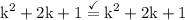
and we are done!
note: the other user is correct but didn't explain the assuming part which can be misleading