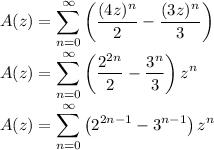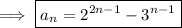Consider the generating function of the sequence
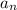 , defined by
, defined by
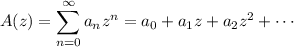
(this is also known as the Z-transform of
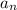 )
)
While the given sequence isn't exactly defined for n = 0, we can use the recurrence to extend it to cover this case. For n = 0, we get
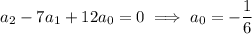
Since for all n ∈ {0, 1, 2, …} we have that
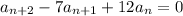
Multiplying both sides by
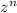 and summing over all n gives the relation
and summing over all n gives the relation
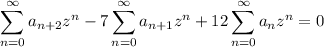
Manipulate the first two series to get them in terms of A(z) :
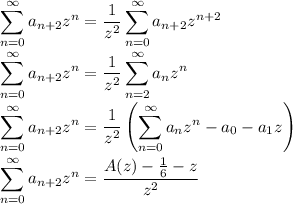
and
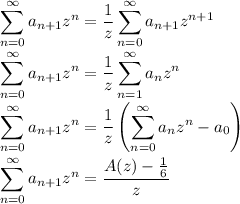
The third series is simply A(z).
Solve this new recurrence for A(z) :
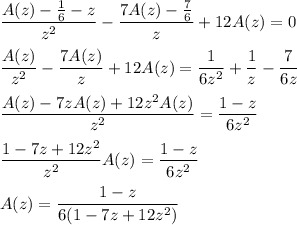
The next step is to find the power series expansion for A(z) to recover
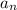 . Factorize the denominator, then decompose A(z) into partial fractions:
. Factorize the denominator, then decompose A(z) into partial fractions:
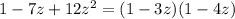
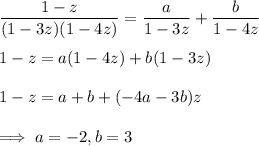
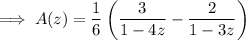
Recall that for |z| < 1, we have
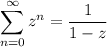
Then if |4z| < 1, we can write A(z) as the sum of two convergent geometric series,
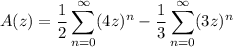
and some rewriting to put this in the canonical G.F. form lets us easily pick out
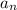 .
.