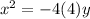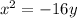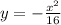Answer:
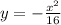
Explanation:
First, notice the diretcrtirx is a negative horinzontal lie so this means we have a parabola facing downwards
Equation of a Parabola with center (h,k) >
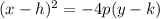
Where p is the distance of the vertex to focus/ or distance to vertex to directrix
This emans that the vertex is halfway of (-4,0) and x=4.
Since this is a upwards parabola, the y value that lies on focal axis doesn't change so know this means that
The vertex is halfway between (-4,0) and (4,0).
So the vertex is (0,0).
Plugging that in we get,

The distance to the vertex or either the focus or directrix is 4 so p=4