Question

Is the statement (3^5)^4 = (3^4)^5 true? Explain your reasoning.

Answer 1

We use the power rule of exponents to find out that both sides of the equation equal 3^20 (or 3486784401).

Explanation:

For this example, we can just use a calculator and find out that both (3^5)^4 and (3^4)^5 are the same value. But how do we know this algebraically?

When dealing with exponents, we must have a good understanding of the properties of exponents before doing any calculations.

For this example, I recognize that the power rule of exponents is being used:

`(a^(m))^(n) = a^(m*n)`

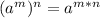
So let's apply this rule to the given equation.

(3^5)^4 = (3^4)^5

3^(5*4) = 3^(4*5)

3^20 = 3^20

Now we know both sides of the equation equal 3^20 (or 3486784401).