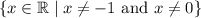(a) Since
![g(x)=\sqrt[3]{x}](https://img.qammunity.org/2022/formulas/mathematics/college/zptkxntlj7hck2dx7g4c7vj149j9c4vigv.png) and
and
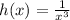 , we have
, we have
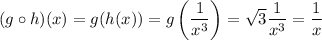
We're given that
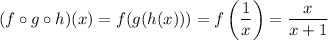
but we can rewrite this as
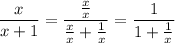
(bear in mind that we can only do this so long as x ≠ 0) so it follows that
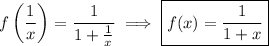
(b) On its own, we may be tempted to conclude that the domain of
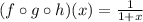 is simply x ≠ -1. But we should be more careful. The domain of a composite depends on each of the component functions involved.
is simply x ≠ -1. But we should be more careful. The domain of a composite depends on each of the component functions involved.
![g(x) = \sqrt[3]{x}](https://img.qammunity.org/2022/formulas/mathematics/college/8kaaatlef2muq8mq5vvj1p62npu6ys0lm5.png) is defined for all x - no issue here.
is defined for all x - no issue here.
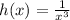 is defined for all x ≠ 0. Then
is defined for all x ≠ 0. Then
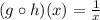 also has a domain of x ≠ 0.
also has a domain of x ≠ 0.
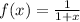 is defined for all x ≠ -1, but
is defined for all x ≠ -1, but
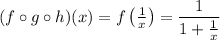
is undefined not only at x = -1, but also at x = 0. So the domain of
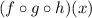 is
is