Consider the contrapositive of the statement you want to prove.
The contrapositive of the logical statement
p ⇒ q
is
¬q ⇒ ¬p
In this case, the contrapositive claims that
"If there are no scalars α and β such that c = αa + βb, then a₁b₂ - a₂b₁ = 0."
The first equation is captured by a system of linear equations,
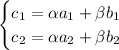
or in matrix form,
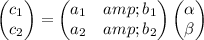
If this system has no solution, then the coefficient matrix on the right side must be singular and its determinant would be
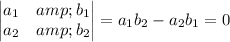
and this is what we wanted to prove. QED