We know,

⠀
Here,
- Diameter of the sphere is 28 m . Therefore, The radius of the sphere is 14 m.
- We will take the value of π as
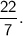
⠀
Substituting the values in the formula :
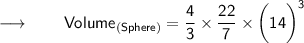
⠀

⠀

⠀

⠀

⠀
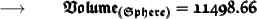
⠀
Therefore,
- Volume of the sphere is about 11500 cubic meters . (Rounded to nearest tenth)