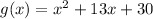Question

The function f(x)=x^2+5x-6 is shifted 4 units to the left to create g(x). What is g(x)

Answer 1

`g(x) = x^2 + 13x + 30`

Explanation:

We are given the function:

`f(x) = x^2 + 5x - 6`

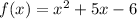
It is shifted 4 units left to create g(x), and we want to determine the equation of g.

Recall that to shift a function horizontally, we add a constant k to the function. k is the horizontal translation. That is:

`\displaystyle f(x) \rightarrow f(x - k)`

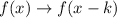
Since we are shifting four units left, k = -4:

`\displaystyle f(x) \rightarrow f(x - (-4)) = f(x+4)`

Find f(x + 4):

`\displaystyle \begin{aligned} g(x) = f(x + 4) &= (x+4)^2 + 5(x+4) - 6 \\ \\ &= (x^2 + 8x + 16) + (5x + 20) - 6 \\ \\ &= (x^2) + (8x + 5x) + (16+20-6) \\ \\&= x^2 + 13x + 30\end{aligned}`

In conclusion:

`g(x) = x^2 + 13x + 30`