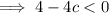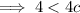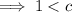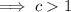Answer:
c > 1
Explanation:
Given equation:
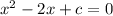
General form of quadratic equation:
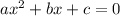
We can use the discriminant to determine the value of c for which the equation has no real roots.
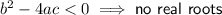
From the given equation:
Inputting these values into the discriminant formula: