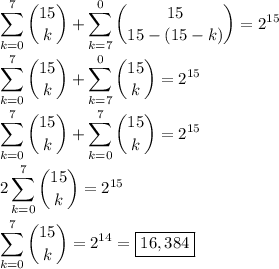Question

How to solve problems like this? I know the answer but I can not find the solution. Thanks

Answer 1

Perhaps the simplest way to compute the sum would just be to evaluate each term in the sum and take the total:

`\displaystyle \sum_(k=0)^7 (15!)/((15-k)!k!) = (15!)/(15!0!) + (15!)/(14!1!) + (15!)/(13!2!) + \cdots + (15!)/(8!7!)`

Then you have

15! / (15! 0!) = 1

15! / (14! 1!) = 15

15! / (13! 2!) = 105

and so on. Adding these results together gives 16,384.

I think a better solution would be to make use of the symmetry of the binomial coefficients, captured by the identity

`\displaystyle \binom nk = \binom n{n-k}`

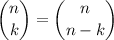
where
`\binom nk = (n!)/((n-k)!k!)`.

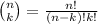By the binomial theorem, we have

`\displaystyle \sum_(k=0)^(15) (15!)/((15-k)!k!) = \sum_(k=0)^(15) \binom{15}k = \sum_(k=0)^(15) \binom{15}k1^k1^(15-k) = (1+1)^(15) = 2^(15)`

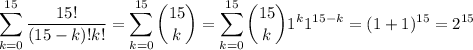
Split up the "complete" sum at k = 7:

`\displaystyle \sum_(k=0)^7 \binom{15}k + \sum_(k=8)^(15)\binom{15}k = 2^(15)`

Use the identity above to rewrite the second sum:

`\displaystyle \sum_(k=0)^7 \binom{15}k + \sum_(k=8)^(15)\binom{15}{15-k} = 2^(15)`

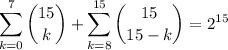
Shift the index on the second sum to make it start at k = 0, and the result follows:

`\displaystyle \sum_(k=0)^7 \binom{15}k + \sum_(k=7)^(0)\binom{15}{15 - (15 - k)} = 2^(15) \\\\ \sum_(k=0)^7 \binom{15}k + \sum_(k=7)^(0)\binom{15}k = 2^(15) \\\\ \sum_(k=0)^7 \binom{15}k + \sum_(k=0)^7\binom{15}k = 2^(15) \\\\ 2\sum_(k=0)^7 \binom{15}k = 2^(15) \\\\ \sum_(k=0)^7 \binom{15}k = 2^(14) = \boxed{16,384}`