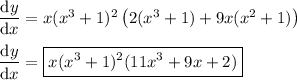Use the product, power, and chain rules.
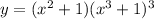
Differentiate both sides:
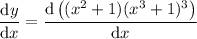
Product rule:
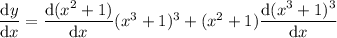
Power rule for the first derivative, power and chain rules for the second one:
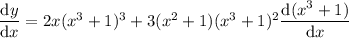
One last applicaton of power rule:
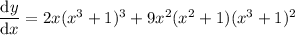
You could stop here, or continue and simplify the result by factorizing: